C++ Greedy Approach Prims MST














































C++ Greedy Approach Prims MST



Prims Minimum Spanning Tree 

Like Kruskals algorithm, Prims algorithm is also a Greedy algorithm. It starts with an empty spanning tree. The idea is to maintain two sets of vertices. The first set contains the vertices already included in the MST, the other set contains the vertices not yet included. At every step, it considers all the edges that connect the two sets, and picks the minimum weight edge from these edges. After picking the edge, it moves the other endpoint of the edge to the set containing MST. 
A group of edges that connects two set of vertices in a graph is called cut in graph theory. So, at every step of Prims algorithm, we find a cut (of two sets, one contains the vertices already included in MST and other contains rest of the vertices), pick the minimum weight edge from the cut and include this vertex to MST Set (the set that contains already included vertices).
How does Prims Algorithm Work? The idea behind Prims algorithm is simple, a spanning tree means all vertices must be connected. So the two disjoint subsets (discussed above) of vertices must be connected to make a Spanning Tree. And they must be connected with the minimum weight edge to make it a Minimum Spanning Tree.
Algorithm 
1) Create a set mstSet that keeps track of vertices already included in MST. 
2) Assign a key value to all vertices in the input graph. Initialize all key values as INFINITE. Assign key value as 0 for the first vertex so that it is picked first. 
3) While mstSet doesn't include all vertices 
        a) Pick a vertex u which is not there in mstSet and has minimum key value.       

        b) Include u to mstSet. 

        c) Update key value of all adjacent vertices of u. To update the key values, iterate through all adjacent vertices. For every adjacent vertex v, if weight of edge u-v is less than the previous key value of v, update the key value as weight of u-v
The idea of using key values is to pick the minimum weight edge from cut. The key values are used only for vertices which are not yet included in MST, the key value for these vertices indicate the minimum weight edges connecting them to the set of vertices included in MST. 
 

 

Let us understand with the following example: 
 

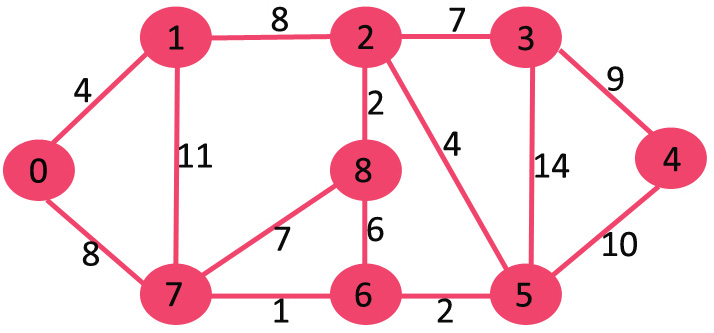
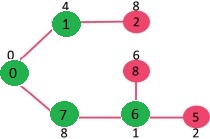
The set mstSet is initially empty and keys assigned to vertices are {0, INF, INF, INF, INF, INF, INF, INF} where INF indicates infinite. Now pick the vertex with the minimum key value. The vertex 0 is picked, include it in mstSet. So mstSet becomes {0}. After including to mstSet, update key values of adjacent vertices. Adjacent vertices of 0 are 1 and 7. The key values of 1 and 7 are updated as 4 and 8. Following subgraph shows vertices and their key values, only the vertices with finite key values are shown. The vertices included in MST are shown in green color.
 

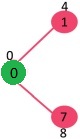
Pick the vertex with minimum key value and not already included in MST (not in mstSET). The vertex 1 is picked and added to mstSet. So mstSet now becomes {0, 1}. Update the key values of adjacent vertices of 1. The key value of vertex 2 becomes 8.
 

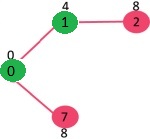
Pick the vertex with minimum key value and not already included in MST (not in mstSET). We can either pick vertex 7 or vertex 2, let vertex 7 is picked. So mstSet now becomes {0, 1, 7}. Update the key values of adjacent vertices of 7. The key value of vertex 6 and 8 becomes finite (1 and 7 respectively). 
 

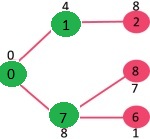
Pick the vertex with minimum key value and not already included in MST (not in mstSET). Vertex 6 is picked. So mstSet now becomes {0, 1, 7, 6}. Update the key values of adjacent vertices of 6. The key value of vertex 5 and 8 are updated.
 

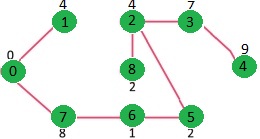
We repeat the above steps until mstSet includes all vertices of given graph. Finally, we get the following graph.
 

How to implement the above algorithm? 
We use a boolean array mstSet[] to represent the set of vertices included in MST. If a value mstSet[v] is true, then vertex v is included in MST, otherwise not. Array key[] is used to store key values of all vertices. Another array parent[] to store indexes of parent nodes in MST. The parent array is the output array which is used to show the constructed MST. 

// A C++ program for Prim's Minimum
// Spanning Tree (MST) algorithm. The program is
// for adjacency matrix representation of the graph
#include <bits/stdc++.h>
using namespace std;

// Number of vertices in the graph
#define V 5

// A utility function to find the vertex with
// minimum key value, from the set of vertices
// not yet included in MST
int minKey(int key[], bool mstSet[])
{
    // Initialize min value
    int min = INT_MAX, min_index;

    for (int v = 0; v < V; v++)
        if (mstSet[v] == false && key[v] < min)
            min = key[v], min_index = v;

    return min_index;
}

// A utility function to print the
// constructed MST stored in parent[]
void printMST(int parent[], int graph[V][V])
{
    cout<<"Edge Weight\n";
    for (int i = 1; i < V; i++)
        cout<<parent[i]<<" - "<<i<<" "<<graph[i][parent[i]]<<" \n";
}

// Function to construct and print MST for
// a graph represented using adjacency
// matrix representation
void primMST(int graph[V][V])
{
    // Array to store constructed MST
    int parent[V];
    
    // Key values used to pick minimum weight edge in cut
    int key[V];
    
    // To represent set of vertices included in MST
    bool mstSet[V];

    // Initialize all keys as INFINITE
    for (int i = 0; i < V; i++)
        key[i] = INT_MAX, mstSet[i] = false;

    // Always include first 1st vertex in MST.
    // Make key 0 so that this vertex is picked as first vertex.
    key[0] = 0;
    parent[0] = -1; // First node is always root of MST

    // The MST will have V vertices
    for (int count = 0; count < V - 1; count++)C
    {
        // Pick the minimum key vertex from the
        // set of vertices not yet included in MST
        int u = minKey(key, mstSet);

        // Add the picked vertex to the MST Set
        mstSet[u] = true;

        // Update key value and parent index of
        // the adjacent vertices of the picked vertex.
        // Consider only those vertices which are not
        // yet included in MST
        for (int v = 0; v < V; v++)

            // graph[u][v] is non zero only for adjacent vertices of m
            // mstSet[v] is false for vertices not yet included in MST
            // Update the key only if graph[u][v] is smaller than key[v]
            if (graph[u][v] && mstSet[v] == false && graph[u][v] < key[v])
                parent[v] = u, key[v] = graph[u][v];
    }

    // print the constructed MST
    printMST(parent, graph);
}

// Driver code
int main()
{
    /* Let us create the following graph
        2 3
    (0)--(1)--(2)
    | / |
    6| 8/  |7
    | / |
    (3)-------(4)
            9    */
    int graph[V][V] = { { 0, 2, 0, 6, 0 },
                        { 2, 0, 3, 8, 5 },
                        { 0, 3, 0, 0, 7 },
                        { 6, 8, 0, 0, 9 },
                        { 0, 5, 7, 9, 0 } };

    // Print the solution
    primMST(graph);

    return 0;
}


Output: 

Edge   Weight
0 - 1    2
1 - 2    3
0 - 3    6
1 - 4    5

Time Complexity of the above program is O(V^2). If the input graph is represented using adjacency list, then the time complexity of Prims algorithm can be reduced to O(E log V) with the help of binary heap.





More Articles of M Mounika:

Name Views Likes
C++ Inplace Rotate square matrix by 90 degrees 834 0
C++ Introduction to Greedy Approach 2611 2
C++ Gold Mine Problem 1432 0
C++ Anagram substring Search 622 0
C++ Segment Trees 912 2
Disjoint Data Structures 636 1
C++ Greedy Approach-Activity Selection Problem 2893 1
C++ Trie Datastructure 3418 1
C++ Minimum Removal of Characters from string to make its permutation as palindrome 650 0
C++ Greedy Approach Minimum number of coins 1788 0
C++ Greedy Approach-Huffman Codes 5654 1
C++ Manachars Algorithm 1978 0
C++ smallest substring with maximum distinct characters 1519 0
C++ Trie Cost of Data 1222 1
C++ Greedy Approach Maximum product Subset 1068 1
C++ Greedy Approach Maximum height Pyramid 1097 1
C++ Greedy Approach-Egyptian Fractions 1551 0
C++ String Matching(KMP Algorithm) 1067 0
C++ K Centers Problem 1286 0
C++ Find Non Repeating Elements in Array 1131 0
C++ Greedy Approach Minimum Product Subset 1236 1
C++ Merge K Sorted Arrays 747 0
C++ Number of Bracket Reversals needed to make expression Balanced 377 0
C++ Basics of String Manipulation 458 1
C++ Problem On Disjoint Data Structures 499 0
C++ Find Nth Catalan Number 1197 0
C++ Greedy Approach String lexicographically largest subsequence 1234 0
C++ Merge Two Binary Trees 737 0
C++ Remove Duplicates From String 3494 0
C++ Minimum characters added at front of string in palindrome conversion 443 0
Disjoint Data Structures Part2 460 0
C++ Greedy Approach Prims MST 1199 1
C++ Greedy Approach N-array maximum sum 810 1
C++ String Matching(Naive Algorithm) 2241 0
C++ Flood Fill Algorithm 3215 0
C++ WildCard pattern matching 3201 0
C++ String Matching(Z Algorithm) 766 0
C++ Meta Strings 738 0
C++ Sum of Numbers From Root To Leaf Paths 713 0
C++ Greedy Approach Lexicographically largest subsequence 978 0
C++ Disjoint Data Structures Part3 417 0
C++ Sieve Of Erastosthenes 569 0
C++ String to Palindrome with Append Function 631 0
C++ Search String in Grid 1715 0
C++ Greedy Approach Policemen Catch Thieves 2376 1
C++ Smallest window with all characters in string 987 0
C++ Greedy Approach Fractional Knapsack 2921 1
C++ Disjoint Data Structure Cycle Detection 605 0
C++ Segmented Sieve (Print Primes In a Range) 2081 0
C++ Greedy Approach Krushkals MST 997 1

Comments